Abstract
A key component for the efficient storage of multiple revisions of a file in fossil repositories is the use of delta-compression, i.e. to store only the changes between revisions instead of the whole file.
This document describes the encoding algorithm used by Fossil to generate deltas. It is targeted at developers working on either fossil itself, or on tools compatible with it. The exact format of the generated byte-sequences, while in general not necessary to understand encoder operation, can be found in the companion specification titled "Fossil Delta Format".
The algorithm is inspired by rsync.
1.0 Arguments, Results, and Parameters
The encoder takes two byte-sequences as input, the "original", and the "target", and returns a single byte-sequence containing the "delta" which transforms the original into the target upon its application.
Note that the data of a "byte-sequence" includes its length, i.e. the number of bytes contained in the sequence.
The algorithm has one parameter named "NHASH", the size of the "sliding window" for the "rolling hash", in bytes. These two terms are explained in the next section. The value of this parameter has to be a power of two for the algorithm to work. For Fossil the value of this parameter is set to "16".
2.0 Operation
The algorithm is split into three phases which generate the header, segment list, and trailer of the delta, per its general structure.
The two phases generating header and trailer are not covered here as their implementation trivially follows directly from the specification of the delta format.
This leaves the segment-list. Its generation is done in two phases, a pre-processing step operating on the "original" byte-sequence, followed by the processing of the "target" byte-sequence using the information gathered by the first step.
2.1 Preprocessing the original
A major part of the processing of the "target" is to find a range in the "original" which contains the same content as found at the current location in the "target".
A naive approach to this would be to search the whole "original" for such content. This however is very inefficient as it would search the same parts of the "original" over and over. What is done instead is to sample the "original" at regular intervals, compute signatures for the sampled locations and store them in a hash table keyed by these signatures.
That is what happens in this step. The following processing step can then the compute signature for its current location and then has to search only a narrow set of locations in the "original" for possible matches, namely those which have the same signature.
In detail:
- The "original" is split into chunks of NHASH bytes. Note that a partial chunk of less than NHASH bytes at the end of "original" is ignored.
- The rolling hash of each chunk is computed.
- A hash table is filled, mapping from the hashes of the chunks to the list of chunk locations having this hash.
2.2 Processing the target
This, the main phase of the encoder, processes the target in a loop from beginning to end. The state of the encoder is captured by two locations, the "base" and the "slide". "base" points to the first byte of the target for which no delta output has been generated yet, and "slide" is the location of the window used to look in the "origin" for commonalities. This window is NHASH bytes long.
Initially both "base" and "slide" point to the beginning of the "target". In each iteration of the loop the encoder decides whether to
- emit a single instruction to copy a range, or
- emit two instructions, first to insert a literal, then to copy a range, or
- move the window forward one byte.
TARGET: [
scale = 0.8
down
"Target" bold
box fill palegreen width 150% height 200% "Processed"
GI: box same as first box fill yellow height 25% "Gap → Insert"
CC: box same fill orange height 200% "Common → Copy"
W: box same as GI fill lightgray width 125% height 200% "Window" bold
box same as CC height 125% ""
box same fill white ""
]
[ "Base" bold ; right ; arrow 33% ] with .e at TARGET.GI.nw
[ "Slide" bold ; right ; arrow 33% ] with .e at TARGET.W.nw
ORIGIN: [
down
"Origin" bold
B1: box fill white
B2: box fill orange height 200%
B3: box fill white height 200%
] with .nw at 0.75 right of TARGET.ne
arrow from TARGET.W.e to ORIGIN.B2.w "Signature" aligned above
→ /pikchrshowTo make this decision the encoder first computes the hash value for the NHASH bytes in the window and then looks at all the locations in the "origin" which have the same signature. This part uses the hash table created by the pre-processing step to efficiently find these locations.
For each of the possible candidates the encoder finds the maximal range of bytes common to both "origin" and "target", going forward and backward from "slide" in the "target", and the candidate location in the "origin". This search is constrained on the side of the "target" by the "base" (backward search), and the end of the "target" (forward search), and on the side of the "origin" by the beginning and end of the "origin", respectively.
There are input files for which the hash chains generated by the pre-processing step can become very long, leading to long search times and affecting the performance of the delta generator. To limit the effect such long chains can have the actual search for candidates is bounded, looking at most N candidates. Currently N is set to 250.
From the ranges for all the candidates the best (= largest) common range is taken and it is determined how many bytes are needed to encode the bytes between the "base" and the end of that range. If the range extended back to the "base" then this can be done in a single copy instruction. Otherwise, i.e if there is a gap between the "base" and the beginning of the range then two instructions are needed, one to insert the bytes in the gap as a literal, and a copy instruction for the range itself. The general situation at this point can be seen in the picture to the right.
If the number of bytes needed to encode both gap (if present), and range is less than the number of bytes we are encoding the encoder will emit the necessary instructions as described above, set "base" and "slide" to the end of the encoded range and start the next iteration at that point.
If, on the other hand, the encoder either did not find candidate locations in the origin, or the best range coming out of the search needed more bytes to encode the range than there were bytes in the range, then no instructions are emitted and the window is moved one byte forward. The "base" is left unchanged in that case.
The processing loop stops at one of two conditions:
- The encoder decided to move the window forward, but the end of the window reached the end of the "target".
- After the emission of instructions the new "base" location is within NHASH bytes of end of the "target", i.e. there are no more than at most NHASH bytes left.
If the processing loop left bytes unencoded, i.e. "base" not exactly at the end of the "target", as is possible for both end conditions, then one last insert instruction is emitted to put these bytes into the delta.
3.0 Exceptions
If the "original" is at most NHASH bytes long no compression of changes is possible, and the segment-list of the delta consists of a single literal which contains the entire "target".
This is actually equivalent to the second end condition of the processing loop described in the previous section, just checked before actually entering the loop.
4.0 The rolling hash
The rolling hash described below and used to compute content signatures was chosen not only for good hashing properties, but also to enable the easy (incremental) recalculation of its value for a sliding window, i.e. where the oldest byte is removed from the window and a new byte is shifted in.
4.1 Definition
Assuming an array Z of NHASH bytes (indexing starting at 0) the hash V is computed via
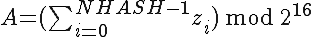
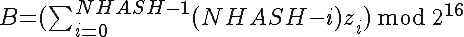
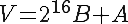
where A and B are unsigned 16-bit integers (hence the mod), and V is a 32-bit unsigned integer with B as MSB, A as LSB.
4.2 Incremental recalculation
Assuming an array Z of NHASH bytes (indexing starting at 0) with
hash V (and components A and B), the dropped
byte 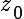 , and the new byte
, and the new byte
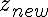 , the new hash can
be computed incrementally via:
, the new hash can
be computed incrementally via:
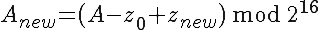
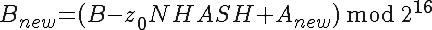
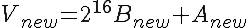
For A, the regular sum, it can be seen easily that this the correct way recomputing that component.
For B, the weighted sum, note first that 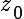 has the weight NHASH in the sum, so that is what has
to be removed. Then adding in
has the weight NHASH in the sum, so that is what has
to be removed. Then adding in 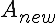 adds one weight factor to all the other values of Z, and at last adds
in
adds one weight factor to all the other values of Z, and at last adds
in 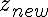 with weight 1, also
generating the correct new sum
with weight 1, also
generating the correct new sum